Flat Points and Scales
In pcf theory we consider the following two orders:
Definition 1. Let $\langle \kappa_n \mid n<\omega \rangle$ be an increasing sequence of uncountable regular cardinals. Their supremum, $\mu$, is a singular cardinal of countable cofinality.
Notice that usually the set of cardinals $A$ that we work with is such that $|A|<\min(A)$. Let $\prod_{n<\omega} \kappa_n := \{ f\mid f:\omega\rightarrow \mu\}$.
For $f,g\in \prod_{n<\omega} \kappa_n$ and $m<\omega$ write $f <_m g$ iff $ f(n) < g(n)$ for all $n>m$. Let $f <^{*} g$ iff for some $f <_m g$ for some $m<\omega$. Similarly we define $f=_m g$ and $f=^{*}g$.
We also write $f < g$ if $f(n) < g(n)$ for all $n<\omega$. Notice that $(\prod_{n<\omega } \kappa_n, <^{*})$ is a quasi-ordered set.
Let $\triangleleft \in \{<, <^{*}\}$.
A sequence $\bar f = \langle f_\alpha \mid \alpha<\lambda\rangle \subseteq \prod_{n<\omega}\kappa_n$ is called $\triangleleft$-increasing if for all $\alpha<\beta<\lambda$ it follows that $f_\alpha \triangleleft f_\beta$.
A sequence $\bar f = \langle f_\alpha \mid \alpha<\lambda\rangle \subseteq \prod_{n<\omega}\kappa_n$ is called $\triangleleft$-cofinal in $\prod_{n<\omega}\kappa_n$ if for all $f\in \prod_{n<\omega}\kappa_n$ there exists $\alpha<\lambda$ so that $f\triangleleft f_\alpha$.
Definition 2. Let $\mu$ be a singular of countable cofinality and let $\mu<\lambda$ be a regular cardinal. A $(\mu,\lambda)$-scale is a pair $(\bar \kappa, \bar f)$ where $\bar \kappa = \langle \kappa_n \mid n<\omega \rangle$ is a strictly increasing sequence of uncountable regular cardinals with $\sup\{\kappa_n \mid n<\omega\}= \mu$ and $\bar f = \langle f_\alpha \mid \alpha<\lambda \rangle \subseteq \prod_{n<\omega} \kappa_n$ is $<^{*}$-increasing and $<^{*}$-cofinal in $\prod_{n<\omega} \kappa_n$.
A function $g:\omega \rightarrow \mathop{\mathrm{On}}$ is an exact upper bound (eub) of a $<^{*}$-increasing sequence $\langle f_\alpha \mid \alpha<\theta \rangle \subseteq {}^\omega \theta$, where $\theta$ is a limit ordinal, if $f_\alpha <^{*} g$ for all $\alpha<\theta$ and for all $h <^{*} g$ there is some $\alpha<\theta$ so that $ h <^{*} f_\alpha$.
The following is a useful Fact.
Fact 3. Suppose $m<\omega$, $\langle \kappa_n\mid n\leq m \rangle$ is a finite sequence of regular cardinals, $\theta$ is a regular cardinal and $\bar t = \langle t_\alpha \mid \alpha<\theta \rangle$ is a sequence in $\prod_{n\leq m}(\kappa_n+1)$.
Then there exists $t\in \prod_{n\leq m} (\kappa_n +1)$ and a cofinal sub-seqence of $\bar t$ that coverges to $t$.
Proof. Successively thin out $\bar t$ using the Pigeon-hole principle so that for each $n\leq m$ the sequence $\langle t_\alpha(n )\mid \alpha<\theta\rangle$ is either constant or strictly increasing of order-type $\theta$. ◻
Lemma 4. Suppose $\bar f =\langle f_\alpha \mid \alpha<\delta \rangle \subseteq {}^{\omega}\mathop{\mathrm{On}}$ is a $ <^{*} $-increasing sequence, $\delta$ is a limit ordinal and $\mathop{\mathrm{cf}}(\delta)=\theta>\aleph_0$. Then the following conditions are equivalent:
There exists an eub $g$ of $\bar f$ so that $\mathop{\mathrm{cf}}(g(n))=\theta$ for all $n<\omega$;
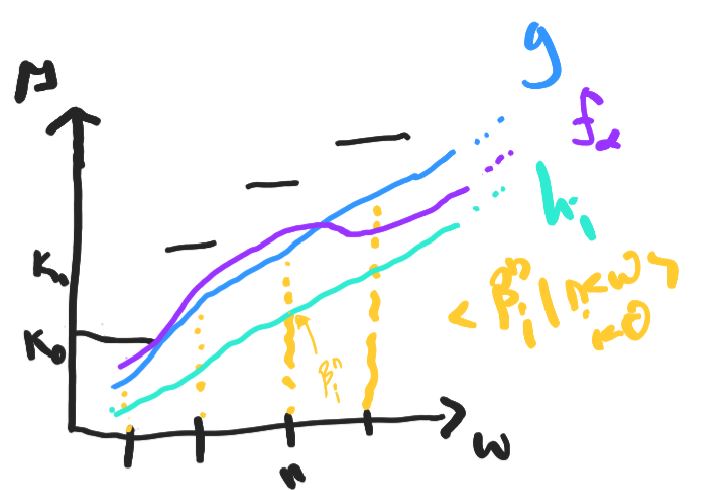
There exists a $<$-increasing sequence $\bar h = \langle h_i \mid i<\theta \rangle \subseteq {}^{\omega}\theta$ so that for every $i<\theta$ there is $\alpha<\delta$ with $ h_i <^{ * } f_\alpha $ and for every $\alpha<\delta$ there is $i<\theta$ with $f_\alpha <^{*} h_i$;
For every unbounded set $C\subseteq \delta$ there is some $m_0<\omega$ and an unbounded set $A\subseteq C$ with $\mathop{\mathrm{otp}}(A) =\theta$ so that $f_\alpha<_{m_0} f_\beta$ for all $\alpha<\beta$ in $A$.
Proof. $(1)\Rightarrow (2):$ Suppose $\bar f$ and $\theta$ are as above and $g$ is an eub of $\bar f$ with $\mathop{\mathrm{cf}}(g(n))=\theta$ for all $n<\omega$.
For each $n<\omega$ we fix a strictly increasing sequence $\langle \beta^n_i \mid i<\theta\rangle$ with supremum $g(n)$.
For $i<\theta$ define a function $h_i:\omega\rightarrow \mathop{\mathrm{On}}$ by $h_i(n):=\beta^n_i$.
Thus, $i< j <\theta$ implies $h_i< h_j$, and $\sup\{ h_i \mid i<\theta\}= g$.
So the sequence $\bar h = \langle h_i \mid i<\theta \rangle$ is $<$-increasing.
Fix $i<\theta$, as $g$ is an eub and $h_i< g$, there is an $\alpha<\delta$ such that $h_i<^{*} f_\alpha$. Fix $\alpha<\delta$, we know that $f_\alpha<^{*}g$.
Hence, there exists some $m<\omega$ such that $f_\alpha<_m g$. For every $m< n <\omega$, there exists some $i_n<\theta$ such that $f_\alpha(n)< h_{i_n}(n)$.
As $\theta$ is regular, there exists some $\sup\{i_n \mid n<\omega\}< i<\theta$.
As $\bar h$ is $<$-increasing, we have that $f_\alpha<^{*} h_i$ as sought.
$(2)\Rightarrow (3):$ Suppose $\bar h = \langle h_i \mid i<\theta \rangle \subseteq {}^{\omega}\theta$ is an $<$-increasing sequence and $C\subseteq \delta$ is an unbounded set.
For each $i<\theta$, let $\alpha(i)\in C$ be chosen such that $h_i<^{*} f_{\alpha(i)}$, $i< j\implies \alpha(i)<\alpha(j)$ and $A$ is unbounded in $C$. Let $A=\{\alpha(i)\mid i<\theta\}$. So $\mathop{\mathrm{otp}}(A)=\theta$.
By recursion over $i<\theta$ we may thin out $\bar h$ such that $f_{\alpha(i)}<^{*} h_{i+1}$. Let $m(i)$ be such that $h_i<_{m(i)}< f_{\alpha(i)} <_{m(i)} h_{i+1}$.
Since $\theta>\aleph_0$ is regular, we may assume, by shrinking $A$ and re-enumerating it increasingly, that there is some fixed $m_0<\omega$ for which $m(i)=m_0$ for all $i<\theta$.
Suppose that $\alpha(i)<\alpha(j)$ are in $A$. Then as required.
$(3)\Rightarrow (1):$ Suppose $A\subseteq \delta$ is unbounded of order-type $\theta$ and $m_0<\omega$ such that for every $\alpha<\beta$ in $A$ implies $f_\alpha <_{m_0} f_\beta$. We define the function $g$ as follows:
Now $g$ is clearly an eub of $\bar f$ and $\mathop{\mathrm{cf}}(g(n))=\theta$ for all $n>m_0$. ◻
A $<^{*}$-increasing $\bar f = \langle f_\alpha \mid \alpha<\delta \rangle$ with $\mathop{\mathrm{cf}}(\delta)=\theta>\aleph_0$ that satisfies one (equivalently, all) of the conditions in the previous Lemma is called flat.
Suppose $(\bar \kappa, \bar f)$ is a $(\mu,\lambda)$-scale for a singular $\mu$ of countable cofinality and a regular $\lambda>\mu$.
An ordinal $\alpha<\lambda$ is called a flat point of $f$ if $\mathop{\mathrm{cf}}(\alpha)>\aleph_0$ and $\bar f\restriction \alpha$ is flat.
A $(\mu,\lambda)$-scale is called good if for all $\alpha<\lambda$ with $\aleph_0<\mathop{\mathrm{cf}}(\alpha)<\mu$, $\alpha$ is a flat pint in $\bar f$ and $f_\alpha$ is an eub of $\bar f \restriction \alpha$.
Theorem 5.
For every $\mu$ singular cardinal of countable cofinality there exists a $(\mu,\mu^+)$-scale in $\mathop{\mathrm{ZFC}}$.
The existence of a supercompact cardinal implies it is consistent there are no good $(\aleph_\omega,\aleph_{\omega+1})$-scales.
$\square_\mu$, and even the weaker prinicple $\mu^+\in I[\mu^+]$, implies the existence of a good $(\mu,\mu^+)$-scale.